Megengedné Isten, hogy a gyerekek rákot kapjanak? Talán...
Megpróbáltam megérteni Karma-kun válaszát a matematikai problémára a vizsga döntőjén.
Kerestem hivatkozásokat és magyarázatokat a problémára, de eredménytelenül. Még mindig nem értettem a probléma borzalmas magyarázatait, és a válasz feltételezi, hogy tudod, hogy gondolkodásuk az, ami nem.
Ez a probléma angol fordítását tartalmazza:
young-il-long-kiyoshi.tumblr.com/post/125623681248/on-the-topic-of-the-final-maths-question-in-the
Egy másik link, amelyen megemlítettem a problémát, de nem magyaráztam meg.
angryanimebitches.com/2016/03/assassination-classroom-season-2-episode-12-the-principal-is-a-sore-loser/
Ezek egy youtube-videó is, amely megmagyarázza Karma-kun válaszát, de még az ő magyarázatát sem tudom még mindig megérteni, hogyan jut arra a következtetésre, hogy a középatom területe megegyezik a kocka területének felével, kettővel osztva. a ^ 3/2
videó link: Furcsa geometria (merénylet Tanterem S2 E12)
Azért teszem közzé ezt, hogy nincs más módja annak, hogy megértsem a problémát anélkül, hogy egy szálon megkérdezném.
Csak a válasz magyarázatát akarom "középiskolai" perspektívában, nem pedig professzionális PhD szintű ...
Nem akarok "egyenlő távolságra", "inifinitesimal", "csúcs" vagy bármilyen más olyan szakkifejezést hallani, amelyet nem értek.
Tudom, hogy túl sokat követelek, de kérem, segítsen megérteni, hogy lett Karma-kun a ^ 3/2. Az egyetlen perspektíva, amelyet a Karmától kaptam, az az, hogy mind a 8 atom egy saját kockát alkot, és ennek a képzeletbeli kockának a középpontja egyenértékű a 8 egyedi kockán belüli összes atomgal.
És a videó is ezt mondja, de hogyan alakult a világban A 1/8 nak nek 2A? és akkor a ^ 3/2
az itt látható módon:
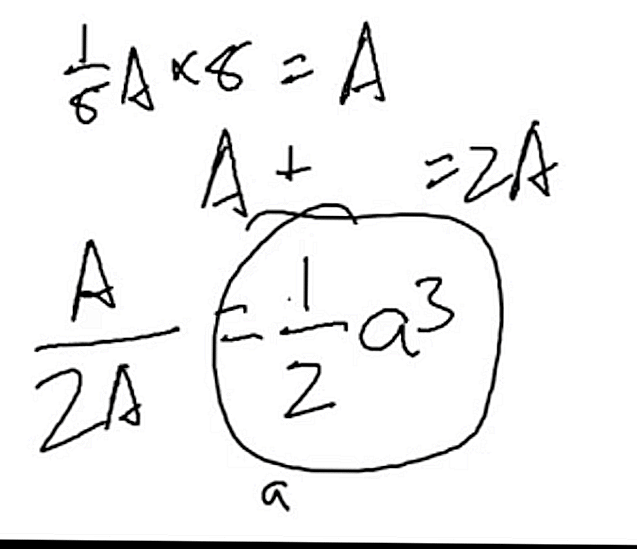
- Asano-kun megoldási módszeréhez szerintem? math.stackexchange.com/questions/3193480/…
A kristályrács összes atomja azonos. Tegyük fel, hogy a csúcsban lévő atom térfogata (nem sarok, ha sarok, akkor kissé más érvelésre lesz szükség) B. A csúcson lévő egyes atomok a kocka (1/8) B részét veszik fel. Lásd a diagramot.
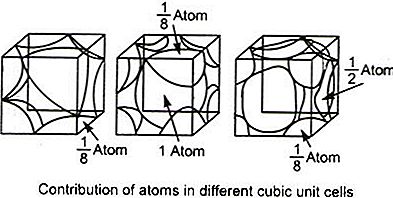
Az a hosszúságú kocka esetében az A központi atomból áll, amelynek térfogata D és 8 atom van a csúcsok csúcsain, mindegyik felveszi (1/8) B kocka. És így,
a3 = D + 8 × (1/8) B
Mivel azonban tudjuk, hogy a csúcsok atomjai valójában megegyeznek a központi atomokkal, a B térfogat egyenlő D-vel és
a3 = B + 8 × (1/8) B ==> B = (1/2) a3
QED
Az összes általad említett szakkifejezés az, amit középiskolámban tanultam. Ez a kérdés nem nehéz, ahogy Karma mondta. Ez a matematika és a kémia együttes kérdése.
7- 1 De azt hiszem, matematikai fórumban kell feltenned, és nem itt. Kínosan néz ki.
- De miért van 2 felett a ^ 3/2 képletben ??
- A több mint 2 itt csak annyit mond, hogy egy kocka esetében a térfogatnak csak a fele lesz az adott A atom által felvett térfogat, a térfogat többi részét meg kell osztani más atomokkal.
- Tehát ha jól követlek, A / 8 * 8 = A, és hogy a nyolc csúcs értéke 2 atomot foglal el, vagyis 2A. akkor azóta A a kocka fele, akkor megtesszük A / 2A... és az atom térfogatának kiszámításához szorozzuk az x, y, z ami 3D és végül megkapjuk a képletet a kocka területének megkeresésére a ^ 3 jobb? akkor úgy felezzük 2 felett? a ^ 3/2
- Nem, a csúcsokban lévő nyolc atom egy atomot foglal el a kockában. Az A / 2A-t használják a központi atom által felvett térfogat arányának a teljes atomhoz és a csúcsokon található atomokhoz viszonyított arányához. Tehát ebből tudjuk, hogy az A atom a kocka térfogatának felét, tehát a ^ 3/2-t veszi fel.
Tudom, hogy elkéstem erről a kérdésről, de itt van egy talán egyszerűbb magyarázat. Éppen eljutottam ehhez a problémához az animékben, és meg akartam oldani, mielőtt felfedték volna a választ.
Rendben. Van egy kocka, amelynek közepén atom van. Amit meg akar tenni, az a kocka nyolc részre törése. Vegyük az egyik ilyen darabot. Két atom van az ellentétes sarkokban (csúcsok). Ezen atomok egyike a központi atom [A] 0, a másik atom a szélén. Egyszerű logika szerint megy, hogy a kocka e nyolcadának pontosan a fele közelebb van az egyik atomhoz, mint a másik. Ez vonatkozik a többi 8 darabra is, így a kocka térfogata a központi atomhoz közelebb egyszerűen a teljes térfogat fele.
A probléma sokkal egyszerűbb, mint amilyennek látszik, és elismerem, hogy a kötetet geometriai darabokkal számoltam, mielőtt rájöttem, hogy néma vagyok. Nem igényel túl sok matematikát. Csak a logika és egy kis okosság megértése.
Állítólag maga a válasz a mangában nem is helyes. Ha az atomok ugyanannyi helyet foglalnak el az egyes kockákon belül, akkor az (a) - a láthatatlan vonalak) felét jelentenék. Lényegében beillesztheti azt a képletet egy gömb térfogatának megoldására, amely négyszer több, mint háromszorosa a p 3-szoros hatványának. Ebben az esetben r (sugara) a / 2 (mert az atomok ugyanazt veszik fel) sok hely, ezért egy atom a láthatatlan vonal felét foglalja el)
Alapvetően V = 4/3 * π * (a / 2) ^ 3
V = 4/3 * π * a ^ 3/8
V = 4 (4/3-ban) törli a 8-at (a ^ 3/8-ban), így 1/3 * π * a ^ 3/2-t kap
V = π * a ^ 3/6
Egyéb: * = idők, ^ = a hatványára, π = pi.